Demo Program Implementasi Algoritma Rock(robust Clustering Using Links) Untuk Menentukan Pola Cluster Pelanggaran Lalu Lintas
10-Juni-2018 - Publish Admin
Algoritma ROCK merupakan suatu algoritma clustering yang mengelompokkan data berbasiskan LINK antar data yang ada. ROCK sendiri adalah singkatan dari RObust Clustering using links. Data yang mempunyai tingkat hubungan (link) tinggi akan digabungkan ke dalam satu cluster, sedang yang mempunyai tingkat hubungan (link) yang kecil akan dipisahkan dari cluster dimana data tersebut dikelompokkan.
Contoh Perhitungan Manual Algoritma ROCK
Mengiput nilai k dan θ
Misalnya menginputkan nilai k = 3dan θ = 0,6
2. Menghitung nilai similaritas antara suatu klaster dengan klaster lainnya, menggunakan rumus jaccard coefficient
Contoh Perhitungan Manual :
Kecamatan
Jenis Kelamin
Usia
Pekerjaan
Pasal & Ancaman Sanksi
6
7
9
13
20
1
7
9
15
20
6
7
9
14
20
6
7
9
14
20
1
7
9
14
20
P dalam rumus maksudnya baris.
P = irisan (banyaknya nilai yang sama) dibagi gabungan (banyak nilai yang sama dihitung 1 + banyak nilai yang berbeda)
Jadi :
nilai sim p1,p2 = 3/7 = 0,248
nilai sim p1,p3 = 4/6 = 0,667
nilai sim p1,p4 = 4/6 = 0,667
nilai sim p1,p5 = 3/7 = 0,248
nilai sim p2,p3 = 3/7 = 0,248
nilai sim p2,p4 = 3/7 = 0,248
nilai sim p2,p5 = 4/6 = 0,667
nilai sim p3,p4 = 5/5 = 1
nilai sim p3,p5 = 4/6 = 0,667
nilai sim p4,p5 = 4/6 = 0,667
nilai sim p5, p5 = 1 (mencari similaritas p itu sendiri = 1 )
bisa juga dilihat di jurnal “Algoritma Rock” halaman 39 – 45 contoh perhitungan algoritma rock..
dibikin matriks
3. Menentukan nilai matrik tetangga (neighbors) Adengan menggunakan nilai-nilai ambang (θ).
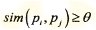
Dengan θ = 0,6 maka cari nilai tetangga antara p1, p2, p3, p4, p5 yang nilai similaritasnya diatas/ lebih besar dari nilai θ maka didapatkan :
Antara garis merah yang merupakan p1 terdapat nilai similaritas yang lebih besar dari nilai θ
Garis biru merupakan nilai similaritas yang lebih besar dari nilai θ
Neighbors [p1] = [p1, p3, p4]
Neighbors [p2] = [p2, p5]
Neighbors [p3] = [p1, p3, p4, p5]
Neighbors [p4] = [p1, p3, p4, p5]
Neighbors [p5] = [p2, p3, p4, p5]
4. Menghitung link antara suatu klaster dengan klaster lainnya. Link(Ti, Tj) antar objek diperoleh dari jumlah tetangga antara Ti dan Tj. Maksudnya menghitung banyaknya neighbors/nilai tetangga antara pi, pj. Atau menghitung banyaknya jumlah irisan antara baris i dan baris j.
Neighbors [p1] = [p1, p3, p4]
Neighbors [p2] = [p2, p5]
Neighbors [p3] = [p1, p3, p4, p5]
Neighbors [p4] = [p1, p3, p4, p5]
Neighbors [p5] = [p2, p3, p4, p5]
Maka didapat :
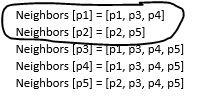
Link (p1,p2) = 0 karena tidak memiliki irisan/ nilai yang sama.
Link (p1,p3) = 3
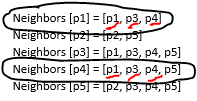
Link (p1,p4) = 3
Link (p1,p5) = 2
Link (p2,p3) = 1
Link (p2,p4) = 1
Link (p2,p5) = 2
Link (p3,p4) = 4
Link (p3,p5) = 3
Link (p4,p5) = 3
Tampilan matriks link :
5. Menghitung nilai goodness measure untuk setiap klaster dengan klaster lainnya jika link != 0 yang disebut local heap
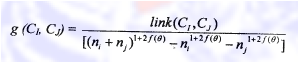
Link(Ci, Cj) = Banyaknya/ nilai link pi,pj
ni = banyaknya anggota i
nj = banyaknya anggota j
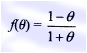maksudnya : 1 – nilai θ yang sudah ditentukan / 1 + nilai θ yang sudah ditentukan
Jadi :
F(θ) = 1- 0,6 / 1+0,6 = 0,25
^ = pangkat
^1+2(F(θ)) = sudah ada dirumus jangan diganti.
Yang diganti hanya nilai ni dan nj, tergantung banyaknya anggota
Hasil dari [(1+1)^1+2(0,25) – 1^1+2(0,25) – 1^1+2(0,25)] yaitu 3,6568542495
6. Memilih nilai maksimum goodness measure antarkolom di baris ke i yang disebut global heap.
Lihat nilai hasil perhitungan goodness measure tadi, kemudian pilih nilai yang tertinggi (global heap) jika ada nilai tinggi yang sama, maka pilih salah satu saja. Dari hasil perhitungan tadi, kita dapatkan nilai tertinggi yaitu pada G(p3,p4) dengan nilai 1,0938. Lalu gabungkan jadi 1 kelompok yaitu p3 dan p4 tadi. Dengan tampilan matriks baru seperti dibawah ini :
7. Ulangi langkah 4, 5 dan 6 hingga mendapatkan nilai maksimum di global heap dan local heap.
Sebelum menghitung langkah ini, terlebih dahulu menggabungkan anggota p3 dan p4 agar dapat menghitung link baru (tahap 5).
Dibawah ini adalah nilai neighbors sebelum menggabungkan p3 dan p4
Neighbors [p1] = [p1, p3, p4]
Neighbors [p2] = [p2, p5]
Neighbors [p3] = [p1, p3, p4, p5]
Neighbors [p4] = [p1, p3, p4, p5]
Neighbors [p5] = [p2, p3, p4, p5]
Dan ini adalah hasil menggabungkan nilai neighbors p3 dan p4
Neighbors [p1] = [p1, p3, p4]
Neighbors [p2] = [p2, p5]
Neighbors [p3,p4] = [p1, p3, p4, p5]
Neighbors [p5] = [p2, p3, p4, p5]
Kemudian cari link baru dengan menggunakan cara yang sama yang ada di tahap 5
Link (p1,p2) = 0
Link (p1,(p3,p4)) = 3
Link (p1,p5) = 2
Link (p2,(p3,p4)) = 1
Link (p2,p5) = 2
Link ((p3,p4),p5) = 3
Kemudian hitung lagi menggunakan rumus yang sama dengan tahap 5.
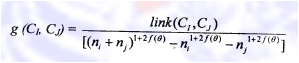
Link(Ci, Cj) = Banyaknya/ nilai link pi,pj
ni = banyaknya anggota i
nj = banyaknya anggota j
Namun nilai yg berubah hanya pada Link Ci, Cj, dan nilai ni dan nj. Nilai tersebut diambil dari nilai link baru diatas.
Kenapa jadi ada (1+2) ? karena banyak anggota Cj ada 2, jika terdapat banyak anggota 3 maka tambahkan saja dengan 3. Tergantung banyak anggota yang ada.
Setelah ditemukan nilai tertinggi dari perhitungan goodess measure tadi, pilih salah satu nilai tertinggi untuk digabungkan. Kita pilih G(p1,(p3,p4)), maka gabungkan baris p1, p3, dan p4 menjadi 1 kelompok.
Matriks link setelah digabung :
Perlu diingat, apabila nilai k yang kita input ada 3, maka perhitungan di stop hingga mendapat 3 kelompok. Disitu sudah otomatis terbentuk 3 kelompok/klaster, yaitu
Kelompok 1 = p1, p3, p4
Kelompok 2 = p2
Kelompok 3 = p5
Apabila nilai k belum dipenuhi maka ulangi lagi langkah 4,5,6 dengan menggunakan cara yang sama hingga semua data sudah masuk didalam anggota k, dan nilai link matriks 0semua atau tidak ada link baru lagi. Jika menggunakan data banyak maka hitung terus hingga nilai link matriks 0 semua atau tidak ada link baru lagi.
8. Selama ukuran data > k, dengan k adalah jumlah kelas yang ditentukan lakukan penggabungan klaster yang memiliki nilai local heap terbesar menjadi satu klaster, tambahkan link antarklaster yang digabungkan, hapus klaster yang digabungkan dari local heap dan update nilai global heap dengan nilai hasil penggabungan.
9. Lakukan langkah 8 hingga menemukan jumlah klaster yang diharapkan atau tidak ada lagi link antara klaster-klasternya
10. Lakukan langkah 1 sampai 10 dengan nilai k dan θ yang berbeda.
Mengiput nilai k dan θ yang berbeda
Misalnya menginputkan nilai k = 3dan θ = 0,5
Menghitung nilai similaritas antara suatu klaster dengan klaster lainnya, menggunakan rumus jaccard coefficient
Contoh Perhitungan Manual :
Kecamatan
Jenis Kelamin
Usia
Pekerjaan
Pasal & Ancaman Sanksi
6
7
9
13
20
1
7
9
15
20
6
7
9
14
20
6
7
9
14
20
1
7
9
14
20
P dalam rumus maksudnya baris.
P = irisan (banyaknya nilai yang sama) dibagi gabungan (banyak nilai yang sama dihitung 1 + banyak nilai yang berbeda)
Jadi :
nilai sim p1,p2 = 3/7 = 0,248
nilai sim p1,p3 = 4/6 = 0,667
nilai sim p1,p4 = 4/6 = 0,667
nilai sim p1,p5 = 3/7 = 0,248
nilai sim p2,p3 = 3/7 = 0,248
nilai sim p2,p4 = 3/7 = 0,248
nilai sim p2,p5 = 4/6 = 0,667
nilai sim p3,p4 = 5/5 = 1
nilai sim p3,p5 = 4/6 = 0,667
nilai sim p4,p5 = 4/6 = 0,667
nilai sim p5, p5 = 1 (mencari similaritas p itu sendiri = 1 )
Menentukan nilai matrik tetangga (neighbors) Adengan menggunakan nilai-nilai ambang (θ).
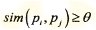
Dengan θ = 0,5 maka cari nilai tetangga antara p1, p2, p3, p4, p5 yang nilai similaritasnya diatas/ lebih besar dari nilai θ maka didapatkan :
Antara garis merah yang merupakan p1 terdapat nilai similaritas yang lebih besar dari nilai θ
Garis biru merupakan nilai similaritas yang lebih besar dari nilai θ
Neighbors [p1] = [p1, p3, p4]
Neighbors [p2] = [p2, p5]
Neighbors [p3] = [p1, p3, p4, p5]
Neighbors [p4] = [p1, p3, p4, p5]
Neighbors [p5] = [p2, p3, p4, p5]
Menghitung link antara suatu klaster dengan klaster lainnya. Link(Ti, Tj) antar objek diperoleh dari jumlah tetangga antara Ti dan Tj. Maksudnya menghitung banyaknya neighbors/nilai tetangga antara pi, pj. Atau menghitung banyaknya jumlah irisan antara baris i dan baris j.
Neighbors [p1] = [p1, p3, p4]
Neighbors [p2] = [p2, p5]
Neighbors [p3] = [p1, p3, p4, p5]
Neighbors [p4] = [p1, p3, p4, p5]
Neighbors [p5] = [p2, p3, p4, p5]
Maka didapat :
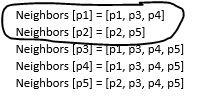
Link (p1,p2) = 0 karena tidak memiliki irisan/ nilai yang sama.
Link (p1,p3) = 3
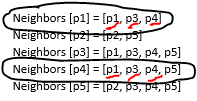
Link (p1,p4) = 3
Link (p1,p5) = 2
Link (p2,p3) = 1
Link (p2,p4) = 1
Link (p2,p5) = 2
Link (p3,p4) = 4
Link (p3,p5) = 3
Link (p4,p5) = 3
Tampilan matriks link :
Menghitung nilai goodness measure untuk setiap klaster dengan klaster lainnya jika link != 0 yang disebut local heap
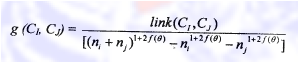
Link(Ci, Cj) = Banyaknya/ nilai link pi,pj
ni = banyaknya anggota i
nj = banyaknya anggota j
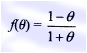maksudnya : 1 – nilai θ yang sudah ditentukan / 1 + nilai θ yang sudah ditentukan
Jadi :
F(θ) = 1- 0,5 / 1+0,5 = 0,33
^ = pangkat
^1+2(F(θ)) = sudah ada dirumus jangan diganti.
Yang diganti hanya nilai ni dan nj, tergantung banyaknya anggota
Hasil dari [(1+1)^1+2(0,33) – 1^1+2(0,33) – 1^1+2(0,33)] yaitu 1,1601
Memilih nilai maksimum goodness measure antarkolom di baris ke i yang disebut global heap.
Lihat nilai hasil perhitungan goodness measure tadi, kemudian pilih nilai yang tertinggi (global heap) jika ada nilai tinggi yang sama, maka pilih salah satu saja. Dari hasil perhitungan tadi, kita dapatkan nilai tertinggi yaitu pada G(p3,p4) dengan nilai 1,0938. Lalu gabungkan jadi 1 kelompok yaitu p3 dan p4 tadi. Dengan tampilan matriks baru seperti dibawah ini :
Ulangi langkah 4, 5 dan 6 hingga mendapatkan nilai maksimum di global heap dan local heap.
Sebelum menghitung langkah ini, terlebih dahulu menggabungkan anggota p3 dan p4 agar dapat menghitung link baru (tahap 5).
Dibawah ini adalah nilai neighbors sebelum menggabungkan p3 dan p4
Neighbors [p1] = [p1, p3, p4]
Neighbors [p2] = [p2, p5]
Neighbors [p3] = [p1, p3, p4, p5]
Neighbors [p4] = [p1, p3, p4, p5]
Neighbors [p5] = [p2, p3, p4, p5]
Dan ini adalah hasil menggabungkan nilai neighbors p3 dan p4
Neighbors [p1] = [p1, p3, p4]
Neighbors [p2] = [p2, p5]
Neighbors [p3,p4] = [p1, p3, p4, p5]
Neighbors [p5] = [p2, p3, p4, p5]
Kemudian cari link baru dengan menggunakan cara yang sama yang ada di tahap 5
Link (p1,p2) = 0
Link (p1,(p3,p4)) = 3
Link (p1,p5) = 2
Link (p2,(p3,p4)) = 1
Link (p2,p5) = 2
Link ((p3,p4),p5) = 3
Kemudian hitung lagi menggunakan rumus yang sama dengan tahap 5.
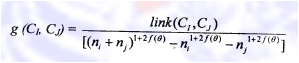
Link(Ci, Cj) = Banyaknya/ nilai link pi,pj
ni = banyaknya anggota i
nj = banyaknya anggota j
Namun nilai yg berubah hanya pada Link Ci, Cj, dan nilai ni dan nj. Nilai tersebut diambil dari nilai link baru diatas.
Kenapa jadi ada (1+2) ? karena banyak anggota Cj ada 2, jika terdapat banyak anggota 3 maka tambahkan saja dengan 3. Tergantung banyak anggota yang ada.
Setelah ditemukan nilai tertinggi dari perhitungan goodess measure tadi, pilih salah satu nilai tertinggi untuk digabungkan. Kita pilih G(p1,p5) maka gabungkan baris p1 dan p5 menjadi 1 kelompok.
Matriks link setelah digabung :
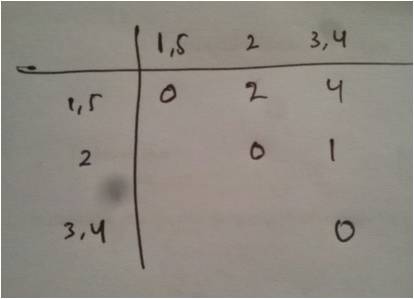
Perlu diingat, apabila nilai k yang kita input ada 3, maka perhitungan di stop hingga mendapat 3 kelompok. Disitu sudah otomatis terbentuk 3 kelompok/klaster, yaitu
Kelompok 1 = p1, p5
Kelompok 2 = p2
Kelompok 3 = p3,p4
Apabila nilai k belum dipenuhi maka ulangi lagi langkah 4,5,6 dengan menggunakan cara yang sama hingga semua data sudah masuk didalam anggota k, dan nilai link matriks 0semua atau tidak ada link baru lagi. Jika menggunakan data banyak maka hitung terus hingga nilai link matriks 0 semua atau tidak ada link baru lagi.
Mengiput nilai k dan θ yang berbeda
Misalnya menginputkan nilai k = 4dan θ = 0,5
Menghitung nilai similaritas antara suatu klaster dengan klaster lainnya, menggunakan rumus jaccard coefficient
Contoh Perhitungan Manual :
Kecamatan
Jenis Kelamin
Usia
Pekerjaan
Pasal & Ancaman Sanksi
6
7
9
13
20
1
7
9
15
20
6
7
9
14
20
6
7
9
14
20
1
7
9
14
20
P dalam rumus maksudnya baris.
P = irisan (banyaknya nilai yang sama) dibagi gabungan (banyak nilai yang sama dihitung 1 + banyak nilai yang berbeda)
Jadi :
nilai sim p1,p2 = 3/7 = 0,248
nilai sim p1,p3 = 4/6 = 0,667
nilai sim p1,p4 = 4/6 = 0,667
nilai sim p1,p5 = 3/7 = 0,248
nilai sim p2,p3 = 3/7 = 0,248
nilai sim p2,p4 = 3/7 = 0,248
nilai sim p2,p5 = 4/6 = 0,667
nilai sim p3,p4 = 5/5 = 1
nilai sim p3,p5 = 4/6 = 0,667
nilai sim p4,p5 = 4/6 = 0,667
nilai sim p5, p5 = 1 (mencari similaritas p itu sendiri = 1 )
Menentukan nilai matrik tetangga (neighbors) Adengan menggunakan nilai-nilai ambang (θ).
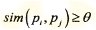
Dengan θ = 0,5 maka cari nilai tetangga antara p1, p2, p3, p4, p5 yang nilai similaritasnya diatas/ lebih besar dari nilai θ maka didapatkan :
Antara garis merah yang merupakan p1 terdapat nilai similaritas yang lebih besar dari nilai θ
Garis biru merupakan nilai similaritas yang lebih besar dari nilai θ
Neighbors [p1] = [p1, p3, p4]
Neighbors [p2] = [p2, p5]
Neighbors [p3] = [p1, p3, p4, p5]
Neighbors [p4] = [p1, p3, p4, p5]
Neighbors [p5] = [p2, p3, p4, p5]
Menghitung link antara suatu klaster dengan klaster lainnya. Link(Ti, Tj) antar objek diperoleh dari jumlah tetangga antara Ti dan Tj. Maksudnya menghitung banyaknya neighbors/nilai tetangga antara pi, pj. Atau menghitung banyaknya jumlah irisan antara baris i dan baris j.
Neighbors [p1] = [p1, p3, p4]
Neighbors [p2] = [p2, p5]
Neighbors [p3] = [p1, p3, p4, p5]
Neighbors [p4] = [p1, p3, p4, p5]
Neighbors [p5] = [p2, p3, p4, p5]
Maka didapat :
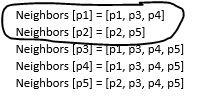
Link (p1,p2) = 0 karena tidak memiliki irisan/ nilai yang sama.
Link (p1,p3) = 3
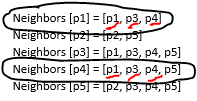
Link (p1,p4) = 3
Link (p1,p5) = 2
Link (p2,p3) = 1
Link (p2,p4) = 1
Link (p2,p5) = 2
Link (p3,p4) = 4
Link (p3,p5) = 3
Link (p4,p5) = 3
Tampilan matriks link :
Menghitung nilai goodness measure untuk setiap klaster dengan klaster lainnya jika link != 0 yang disebut local heap
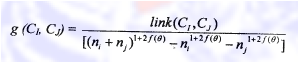
Link(Ci, Cj) = Banyaknya/ nilai link pi,pj
ni = banyaknya anggota i
nj = banyaknya anggota j
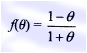maksudnya : 1 – nilai θ yang sudah ditentukan / 1 + nilai θ yang sudah ditentukan
Jadi :
F(θ) = 1- 0,5 / 1+0,5 = 0,33
^ = pangkat
^1+2(F(θ)) = sudah ada dirumus jangan diganti.
Yang diganti hanya nilai ni dan nj, tergantung banyaknya anggota
Hasil dari [(1+1)^1+2(0,33) – 1^1+2(0,33) – 1^1+2(0,33)] yaitu 1,1601
Memilih nilai maksimum goodness measure antarkolom di baris ke i yang disebut global heap.
Lihat nilai hasil perhitungan goodness measure tadi, kemudian pilih nilai yang tertinggi (global heap) jika ada nilai tinggi yang sama, maka pilih salah satu saja. Dari hasil perhitungan tadi, kita dapatkan nilai tertinggi yaitu pada G(p3,p4) dengan nilai 1,0938. Lalu gabungkan jadi 1 kelompok yaitu p3 dan p4 tadi. Dengan tampilan matriks baru seperti dibawah ini :
Perlu diingat, apabila nilai k yang kita input ada 4, maka perhitungan di stop hingga mendapat 4 kelompok. Disitu sudah otomatis terbentuk 4 kelompok/klaster, yaitu
Kelompok 1 = p1
Kelompok 2 = p2
Kelompok 3 = p3,p4
Kelompok 4 = p5
Apabila nilai k belum dipenuhi maka ulangi lagi langkah 4,5,6 dengan menggunakan cara yang sama hingga semua data sudah masuk didalam anggota k, dan nilai link matriks 0semua atau tidak ada link baru lagi. Jika menggunakan data banyak maka hitung terus hingga nilai link matriks 0 semua atau tidak ada link baru lagi.
Lakukan perhitungan cohesion dan separation untuk mengetahui pola cluster terbaik.
Setelah menghitung beberapa cluster/Kelompok
Didapat :
k = 3 dan θ = 0,6
Kelompok 1 = p1, p3, p4
Kelompok 2 = p2
Kelompok 3 = p5
k = 3dan θ = 0,5
Kelompok 1 = p1, p5
Kelompok 2 = p2
Kelompok 3 = p3,p4
k = 4dan θ = 0,5
Kelompok 1 = p1
Kelompok 2 = p2
Kelompok 3 = p3,p4
Kelompok 4 = p5
Maka cari klaster terbaik dengan menggunakan cohesion dan separation :
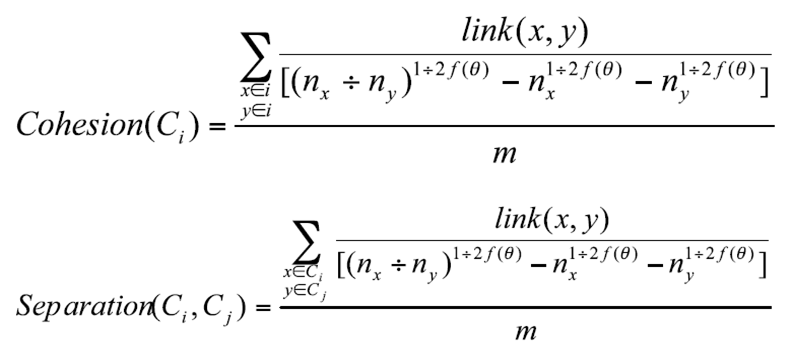
Dengan nilai
Menghitung nilai cohesion dan separationk = 3 dan θ = 0,6
Kelompok/ klaster
Jumlah Anggota
Anggota
Cohesion
Separation
1
3
p1, p3, p4
Hasil didapat dari perhitungan goodness measure sebelumnya (jika ada) (bisa diliat di perhitungan goodness measure sebelumnya dimana terdapat anggota klaster 1 pada perhitungan nilai goodness measure. G(p1,(p3,p4)) = 3 / [(1+2)^1+2(0,25) – 1^1+2(0,25) – 2^1+2(0,25)] = 2,1934
Hasil didapat dari perhitungan goodness measure sebelumnya (jika ada).
Perhitugan diatas dapat dilakukan dengan cara menambahkan semua nilai goodness measure yang terhubung kemudian dibagi dengan jumlah anggota yang terhubung antar cluster.
Hitung (tambahkan) nilai godness measure antara klaster 1 dan klaster 2, kluster 1 dan kluster 3, klaster 2 dan klaster 3 kemudian bagi dengan jumlah anggota sudah berpasangan.
[(1+1)^1+2(0,25) – 1^1+2(0,25) – 1^1+2(0,25)] merupakan hasil perhitungan dari
Jadi jika hanya memiliki satu anggota, maka hitung nilai goodness measure anggota itu sendiri menggunakan rumus :
Link(Ci, Cj) = Banyaknya/ nilai link pi
ni = banyaknya anggota i
nj = banyaknya anggota i
Lalu setelah didapat nilai klaster 1, 2, dan 3 kemudian ditambah keseluruhan lalu bagi dengan jumlah kalster (rata-rata)
= (klaster 1 + klaster 2 + klaster 3) / 3
= (2,1934 + 0,2734 + 0,2734) / 3
= 2,7402 / 3
= 0,9134
3
1
p5
Jadi nilai cohesion dan separation pada k = 3 dan θ = 0,6 yaitu
Cohesion
Separation
0,9134
0,1562
Menghitung nilai cohesion dan separationk = 3 dan θ = 0,5
Kelompok/ klaster
Jumlah Anggota
Anggota
Cohesion
Separation
1
2
p1, p5
Hasil didapat dari perhitungan goodness measure sebelumnya (jika ada) (bisa diliat di perhitungan goodness measure sebelumnya dimana terdapat anggota klaster 1 pada perhitungan nilai goodness measure. G(p1,p5) = 2 / [(1+1)^1+2(0,33) – 1^1+2(0,33) – 1^1+2(0,33)] = 1,7238
Hasil didapat dari perhitungan goodness measure sebelumnya (jika ada).
Perhitugan diatas dapat dilakukan dengan cara menambahkan semua nilai goodness measure yang terhubung kemudian dibagi dengan jumlah anggota yang terhubung antar cluster.
Hitung (tambahkan) nilai godness measure antara klaster 1 dan klaster 2, kluster 1 dan kluster 3, klaster 2 dan klaster 3 kemudian bagi dengan jumlah anggota sudah berpasangan.
[(1+1)^1+2(0,33) – 1^1+2(0,33) – 1^1+2(0,33)] merupakan hasil perhitungan dari
Jadi jika hanya memiliki satu anggota, maka hitung nilai goodness measure anggota itu sendiri menggunakan rumus :
Link(Ci, Cj) = Banyaknya/ nilai link pi
ni = banyaknya anggota i
nj = banyaknya anggota i
3
2
p3, p4
Hasil didapat dari perhitungan goodness measure sebelumnya (jika ada) (bisa diliat di perhitungan goodness measure sebelumnya dimana terdapat anggota klaster 1 pada perhitungan nilai goodness measure. G(p3,p4) = 4 / [(1+1)^1+2(0,33) – 1^1+2(0,33) – 1^1+2(0,33)] = 3,4477
Lalu setelah didapat nilai klaster 1, 2, dan 3 kemudian ditambah keseluruhan lalu bagi dengan jumlah kalster (rata-rata)
= (klaster 1 + klaster 2 + klaster 3) / 3
= (1,7238 + 0,8619 + 3,4477) / 3
= 6,0334 / 3
= 2,0111
Jadi nilai cohesion dan separation pada k = 3 dan θ = 0,5 yaitu
Cohesion
Separation
2,0111
0,5558
Menghitung nilai cohesion dan separationk = 4 dan θ = 0,5
Kelompok/ klaster
Jumlah Anggota
Anggota
Cohesion
Separation
1
1
p1
Jika hanya memiliki 1 anggota maka, hitung nilai goodness measure anggota itu sendiri yaitu
Perhitugan diatas dapat dilakukan dengan cara menambahkan semua nilai goodness measure yang terhubung kemudian dibagi dengan jumlah anggota yang terhubung antar cluster.
Hitung (tambahkan) nilai godness measure antara klaster 1 dan klaster 2, kluster 1 dan kluster 3, klaster 2 dan klaster 3 kemudian bagi dengan jumlah anggota sudah berpasangan.
[(1+1)^1+2(0,33) – 1^1+2(0,33) – 1^1+2(0,33)] merupakan hasil perhitungan dari
Jadi jika hanya memiliki satu anggota, maka hitung nilai goodness measure anggota itu sendiri menggunakan rumus :
Link(Ci, Cj) = Banyaknya/ nilai link pi
ni = banyaknya anggota i
nj = banyaknya anggota i
3
2
p3,p4
Hasil didapat dari perhitungan goodness measure sebelumnya (jika ada) (bisa diliat di perhitungan goodness measure sebelumnya dimana terdapat anggota klaster 1 pada perhitungan nilai goodness measure. G(p3,p4) = 4 / [(1+1)^1+2(0,33) – 1^1+2(0,33) – 1^1+2(0,33)] = 3,4477
4
1
p5
Jika hanya memiliki 1 anggota maka, hitung nilai goodness measure anggota itu sendiri yaitu
Jadi nilai cohesion dan separation pada k = 4 dan θ = 0,5 yaitu
Cohesion
Separation
1,5084
0,5746
k
θ
Cohesion
Separation
Hasil Akhir Selisih nilai cohesion dan separaton
(Cohesion – Separation)
3
0,6
0,9134
0,1562
0,7572
3
0,5
2,0111
0,5558
1,4553
4
0,5
1,5084
0,5746
0,9338
Semakin tinggi nilai cohesion dan semakin minimum nilai separation maka semakin baik suatu cluster terhadap yang lainnya. Jadi dapat kita lihat dari data tersebut :
Setelah didapat nilai cohesion dan separation, maka cluster terbaik yaitu k=3 dan θ=0,5 dengan anggota cluster
cluster 1 = p1, p5
cluster 2 = p2
cluster 3 = p3,p4
cara membaca anggota cluster : yang paling dominan muncul dalam 1 baris ke baris lainnya
misalnya :
pada cluster 1 merupakan pelanggar lalu lintas yang berasal dari kecamatan luar banjarbaru dan landasan ulin, jenis kelamin laki-laki, dengan usia dewasa awal yaitu usia 12 tahun hingga 15 tahun, yang memiliki pekerjaan swasta, dan telah melanggar lalu lintas kategori ringan dimana ancaman sanksi yang didapat yaitu kurungan < 2 bulan atau denda <Rp. 500.000
Shared
Shared
Shared
Shared
maksudnya : 1 – nilai θ yang sudah ditentukan / 1 + nilai θ yang sudah ditentukan
