Demo Program Peramalan Prediksi Kasus Demam Berdarah Algoritma Singel Exponential Smoothing
28-Juni-2018 - Publish Admin
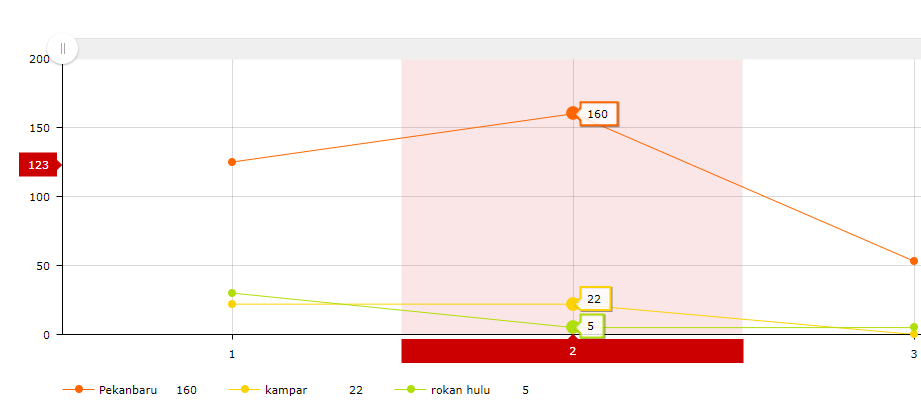
Menurut Render dan Heizer (2005) Penghalusan exponential adalah teknik peramalan rata-rata bergerak dengan pembobotan dimana data diberi bobot oleh sebuah fungsi exponential. Penghalusan exponential merupakan metode peramalan rata-rata bergerak dengan pembobotan canggih, namun masih mudah digunakan. Metode ini sangat dedikit pencatatan data masa lalu. Rumus penghalusan exponential dapat ditunjukkan sebagai berikut :
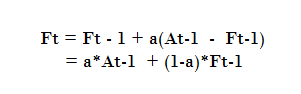
Ft+1= α Xt + (1-α) Ft-1
Keterangan :
Ft+1 = Ramalan untuk periode ke t+1 Xt = Nilai riil periode ke t+1
Xt = Nilai riil periode ke t
α = Bobot yang menunjukkan konstanta penghalus (0 < α <1)
Ft-1 = Ramalan untuk periode ke t-1
Metode ini membutuhkan nilai alpha (α) sebagai nilai parameter pemulusan. Bobot nilai α lebih tinggi diberikan kepada data yang lebih baru, sehingga nilai parameter α yang sesuai akan memberikan ramalan yang optimal dengan nilai kesalahan (error) terkecil. Untuk mendapatkan nilai α yang tepat pada umumnya dilakukan dengan trial and error (coba-coba) untuk menentukan nilai kesalahan terendah. Nilai α dilakukan dengan membandingkan menggunakan interval pemulusan antar 0 < α < 1, yaitu α (0,1 sampai dengan 0,9). Metode ini hanya mampu memberikan ramalan satu periode ke depan dan cocok untuk data yang mengandung unsur stationer. Karena jika diterapkan pada serial data yang memiliki trend yang konsisten, ramalan yang dibuat akan selalu berada dibelakang trend. Selain itu, metode eksponensial ini juga memberikan bobot yang relatif lebih tinggi pada nilai pengamatan terbaru dibanding nilai-nilai periode sebelumnya.
Proses Perhitungan Menggunakan Metode Single Exponential Smoothing
Sampel Data
|
No |
Tahun |
Bulan |
Jumlah |
|
1 |
2015 |
Januari |
125 |
|
2 |
2015 |
Februari |
160 |
|
3 |
2015 |
Maret |
53 |
Dalam peramalan ini, alpha (α) yang akan dicoba (trial) secara acak sebagai nilai bobot dan contoh perhitungan adalah (α = 0.1), (α = 0.2), (α = 0.3), (α = 0.4), (α = 0.5), (α = 0.6), (α = 0.7), (α = 0.8), dan (α = 0.9).
- Berikut contoh perhitungan untuk konstanta alpha (α = 0.1)
F1 = Karena pada saat t=1 nilai F1 (peramalan pada periode pertama) belum tersedia, maka untuk mengatasi masalah ini dapat dilakukan dengan menetapkan nilai F1 sama dengan nilai data periode pertama (X1) sebesar 125
F1 = 125
F2 = α X1 + (1- α)F1
= (0.1 * 160) + (1 - 0.1)*125
= 128.5
F3 = α X2 + (1- α)F2
= (0.1 * 53) + (1 - 0.1)*128.5
= 120.95
- Berikut contoh perhitungan untuk konstanta alpha (α = 0.2)
F1 = 125
F2 = α X1 + (1- α)F1
= (0.2 * 160) + (1 - 0.2)*125
= 132
F3 = α X2 + (1- α)F2
= (0.2 * 53) + (1 - 0.1)*132
= 116.2
- Berikut contoh perhitungan untuk konstanta alpha (α = 0.3)
F1 = 125
F2 = α X1 + (1- α)F
= (0.3 * 160) + (1 - 0.3)*125
= 135.5
F3 = α X2 + (1- α)F2
= (0.3 * 53) + (1 - 0.3)*135.5
= 110.75
- Berikut contoh perhitungan untuk konstanta alpha (α = 0.4)
F1 = 125
F2 = α X1 + (1- α)F1
= (0.4 * 160) + (1 - 0.4)*125
= 139
F3 = α X2 + (1- α)F2
= (0.4 * 53) + (1 - 0.4)*139
= 104.6
- Berikut contoh perhitungan untuk konstanta alpha (α = 0.5)
F1 = 125
F2 = α X1 + (1- α)F1
= (0.5 * 160) + (1 - 0.5)*125
= 142.5
F3 = α X2 + (1- α)F2
= (0.5 * 53) + (1 - 0.5)*142.5
= 97.75
- Berikut contoh perhitungan untuk konstanta alpha (α = 0.6)
F1 = 125
F2 = α X1 + (1- α)F1
= (0.6 * 160) + (1 - 0.6)*125
= 146
F3 = α X2 + (1- α)F2
= (0.6 * 53) + (1 - 0.6)*146
= 90.2
- Berikut contoh perhitungan untuk konstanta alpha (α = 0.7)
F1 = 125
F2 = α X1 + (1- α)F1
= (0.7 * 160) + (1 - 0.7)*125
= 149.5
F3 = α X2 + (1- α)F2
= (0.7 * 53) + (1 - 0.7)*149.5
= 81.95
- Berikut contoh perhitungan untuk konstanta alpha (α = 0.8)
F1 = 125
F2 = α X1 + (1- α)F1
= (0.8 * 160) + (1 - 0.8)*125
= 153
F3 = α X2 + (1- α)F2
= (0.8 * 53) + (1 - 0.8)*153
= 73
- Berikut contoh perhitungan untuk konstanta alpha (α = 0.9)
F1 = 125
F2 = α X1 + (1- α)F1
= (0.9 * 160) + (1 - 0.9)*125
= 156.5
F3 = α X2 + (1- α)F2
= (0.9 * 53) + (1 - 0.9)*156.5
= 63.35
|
No |
Bulan |
Jumlah |
0.1 |
0.2 |
0.3 |
0.4 |
0.5 |
0.6 |
0.7 |
0.8 |
0.9 |
|
1 |
Januari |
125 |
|
|
|
|
|
|
|
|
|
|
2 |
Februari |
160 |
125 |
125 |
125 |
125 |
125 |
125 |
125 |
125 |
125 |
|
3 |
Maret |
53 |
128.5 |
132 |
135.5 |
139 |
142.5 |
146 |
149.5 |
153 |
156.5 |
|
4 |
April |
|
120.95 |
116.2 |
110.75 |
104.6 |
97.75 |
90.2 |
81.95 |
73 |
63.35 |
Karena nilai 120.95 lebih besar dari pada nilai yang lain, maka hasil peramalan pada bulan april yaitu : 120.95
Contoh Skript Metode Singel Exponentioal Smoothing
$dt=mysql_query("SELECT * from tabel_kasus inner join tabel_kabupaten on tabel_kasus.kode_kabupaten=tabel_kabupaten.kode_kabupaten where tabel_kabupaten.kode_kabupaten='$hsl[kode_kabupaten]' order by tabel_kasus.bulan");
while ($rst=mysql_fetch_array($dt)) {
if ($rst['bulan']=="01") {$bulan = "Januari";}elseif ($rst['bulan']=="02") {$bulan = "Februari";}elseif ($rst['bulan']=="03") {$bulan = "Maret";}elseif ($rst['bulan']=="04") {$bulan = "April";}elseif ($rst['bulan']=="05") {$bulan = "Mei";}elseif ($rst['bulan']=="06") {$bulan = "Juni";}elseif ($rst['bulan']=="06") {$bulan = "Juli";}elseif ($rst['bulan']=="07") {$bulan = "Juli";}elseif ($rst['bulan']=="08") {$bulan = "Agustus";}elseif ($rst['bulan']=="09") {$bulan = "September";}elseif ($rst['bulan']=="10") {$bulan = "Oktober";}elseif ($rst['bulan']=="11") {$bulan = "November";}elseif ($rst['bulan']=="12") {$bulan = "Desember";}
$bln=$rst['bulan'];
$thn=$rst['tahun'];
echo "
$no
$rst[tahun]
$bulan
$rst[jumlah] ";
$jl[$n][$no] = $rst['jumlah'];
$nm=$no-1;
if ($no>1) {
if ($no == 2) {
$error_singel1="";
$dl1="";
foreach ($deta as $key => $value) {
$hsl1="";
$nilai[$no][$key]=$jl[$n][$no-1];
$hsl1 = $nilai[$no][$key]-$rst['jumlah'];
$hslak1 = $hsl1*$hsl1;
$nl1[$key][] = $hslak1;
echo " ".round($nilai[$no][$key],2)." ";
}
}
else{
$error_singel1="";
$dl1="";
foreach ($deta as $key => $value) {
$hsl1="";
$nilai[$no][$key]=($value*$jl[$n][$no-1])+((1-$value)*$nilai[$no-1][$key]);
$hsl1 = $nilai[$no][$key]-$rst['jumlah'];
$hslak1 = $hsl1*$hsl1;
$nl1[$key][] = $hslak1;
echo " ".round($nilai[$no][$key],2)."";//."
Rumus
(".$value."*".$jl[$n][$no-1].")+((1-".$value.")*".$nilai[$no-1][$key].")"." ";
// = "(".$value."*".$jl[$n][$no-1].")+((1-".$value.")*".$nilai[$no-1][$key].")"
}
}
}
else{
foreach ($deta as $key => $value) {
echo "
$no
$thn
$bulan1
".round($nilai[$no][$key],2)."";//."
rumus = (".$value."*".$jl[$n][$no-1].")+((1-".$value.")*".$nilai[$no-1][$key].") ";
// = "(".$value."*".$jl[$n][$no-1]."")+((1-".$value.")*".$nilai[$no-1][$key].")"
$prm[] = round($nilai[$no][$key],2);
}
foreach ($deta as $key => $value) {
//$ttl1="";
$ttl1[$key] = array_sum($nl1[$key])/($no-2);
$del[$ttl1[$key]] = $value;
//echo " ".$ttl1[$key]." ";
// = "."((".$value."*".$jl[$n][$no1-1].")+(1-".$value."))+".$nilai[$no1-1][$key]."
}
//foreach ($prm as $key => $value) {
if ($del[min($ttl1)]=="0.1") {
$hslnya = $prm['0'];
}
elseif ($del[min($ttl1)]=="0.2") {
$hslnya = $prm['1'];
}
elseif ($del[min($ttl1)]=="0.3") {
$hslnya = $prm['2'];
}
elseif ($del[min($ttl1)]=="0.4") {
$hslnya = $prm['3'];
}
elseif ($del[min($ttl1)]=="0.5") {
$hslnya = $prm['4'];
}
elseif ($del[min($ttl1)]=="0.6") {
$hslnya = $prm['5'];
}
elseif ($del[min($ttl1)]=="0.7") {
$hslnya = $prm['6'];
}
elseif ($del[min($ttl1)]=="0.8") {
$hslnya = $prm['7'];
}
elseif ($del[min($ttl1)]=="0.9") {
$hslnya = $prm['8'];
}
// }
Judul Skripsi Lainnya
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
;
Sistemit24.com

Bingung Dengan Algoritma?
Jangan kawatir Sistemit24.com dapat membantu kalian dalam membuat tugas akhir, Dijamin sampai benar-benar selesai.
- Tidak ada batasan untuk revisi
- Dibimbing sampai benar-benar faham
Kami dapat membuatkan dari awal sampai selesai.
Berminat? bisa hubungi kami lewat email : [email protected] Atau hubungi lewat wa 0823-8560-3528
Loading…
 Shared
Shared
 Shared
Shared
 Shared
Shared
 Shared
Shared