Demo Program Analisa Algoritma Complete Linkage Untuk Penentuan K Optimal Pada Cluster
10-Juni-2018 - Publish Admin
Complete Linkage Method adalah metode pengklasteran yang didasarkan jarak yang paling maksimum antar objek. Dua objek yang dibandingkan yaitu objek pertama yang mempunyai jarak euclidean terkecil, dengan objek kedua yang memiliki jarak terjauh dari objek pertama. Jika dua objek tersebut, terpisah oleh jarak yang jauh, maka kedua objek tersebut akan digabung menjadi satu klaster, demikian seterusnya.
Langkah ketiga untuk algoritma metode ini berbeda dengan algoritma Single Linkage Method, pada langkah ketiga metode ini dari klaster UV yang terbentuk kemudian dicari jarak maksimum antar klaster UV dengan objek-objek berada di luar klaster UV, misalkan d(uv)w = max (duw,dvw). Dari langkah ketiga ini akan diperoleh matriks jarak baru D(2) dan selanjutnya ulangi langkah kedua sampai semua objek bergabung menjadi satu kelompok.
Simulasi Perhitungan Algoritma
Contoh Data
| No | Daya x | Data Y |
|---|---|---|
| 1 | 1 | 1 |
| 2 | 4 | 1 |
| 3 | 1 | 2 |
| 4 | 3 | 4 |
| 5 | 5 | 4 |
Algoritma Complete Linkage
1. Tentukan Jarak Kedekatan antar data Menggunakan Euclidean Distance
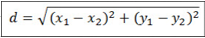
| Euclidean Distance | Hasil |
|---|---|
| Jarak Data 1 ke 2 | 3,00 |
| Jarak Data 1 ke 3 | 1,00 |
| Jarak Data 1 ke 4 | 3,61 |
| Jarak Data 1 ke 5 | 5,00 |
| Jarak Data 2 ke 3 | 3,16 |
| Jarak Data 2 ke 4 | 3,16 |
| Jarak Data 2 ke 5 | 3,16 |
| Jarak Data 3 ke 4 | 2,83 |
| Jarak Data 3 ke 5 | 4,47 |
| Jarak Data 4 ke 5 | 2,00 |
2. Buat Tabel Kedekatan Antar Data
| DEuclidean | 1 | 2 | 3 | 4 | 5 |
| 1 | 0 | 3 | 1 | 3,61 | 5 |
| 2 | 3 | 0 | 3,16 | 3,16 | 3,16 |
| 3 | 1 | 3,16 | 0 | 2,83 | 4,47 |
| 4 | 3,61 | 3,16 | 2,83 | 0 | 2 |
| 5 | 5 | 3,16 | 4,47 | 2 | 0 |
3. Pertama kita cari Jarak terkecil dari tabel jarak diatas
min(DEuclidean) = min (D13) = 1
Jarak terkecil dimilik kelompok 1 dan 3, sehingga kelompok 1 dan 3 digabungkan
4. Masuk ke Algoritma Complete Linkage
Yaitu menghitung jarak antar data yang terkecil yaitu (D13) dengan data selainnya yaitu data 2, 4 dan 5
Rumus Complete Linkage
min(DEuclidean)data selainnya = max ((D(x)Euclidean.data selainnya), (D(y)Euclidean.data selainnya))
dalam hal ini D(Euclidean) = D(13)
Jadi :
D(13)2 = max(D(12), D(32)) = max (3 , 3.16) = 3.16
D(13)4 = max(D(14), D(34)) = max (3.61 , 2.83) = 3.61
D(13)5 = max(D(15), D(35)) = max (5 , 4.47) = 5
5. Dengan menghapus baris-baris dan kolom-kolom matrik jarak yang bersesuaian dengan kelompok 1 dan 3 serta menambahkan baris dan kolom untuk kelompok (13).
| DEuclidean | D(13) | 2 | 4 | 5 |
| D(13) | 0 | 3,16 | 3,61 | 5 |
| 2 | 3,16 | 0 | 3,16 | 3,16 |
| 4 | 3,61 | 3,16 | 0 | 2 |
| 5 | 5 | 3,16 | 2 | 0 |
6. Ulangi Langkah 3 sampai 5 hingga menyisakan kelompok tunggal
min D(Euclidean) = D(45) = 2
Jadi :
D(45)13 = max(D(41), D(43),D(51), D(53)) = max (3.61, 2.83, 5, 4.47) = 5
D(45)2 = max(D(42), D(52)) = max (3.16 , 3.16) = 3.16
| DEuclidean | D(45) | D(13) | 2 |
| D(45) | 0 | 5 | 3,16 |
| D(13) | 5 | 0 | 3,16 |
| 2 | 3,16 | 3,16 | 0 |
min D(Euclidean) = D((45)2) = 3.16
Jadi :
D(452)13 = max(D(41), D(43),D(51), D(53), D(21), D(23)) = max (3.61, 2.83, 5, 4.47, 3, 3.16 ) = 5
| DEuclidean | D(452) | D(13) |
| D(452) | 0 | 5 |
| D(13) | 5 | 0 |
Jadi kelompok (452) dan (13) digabung untuk menjadi kelompok tunggal dari lima data, yaitu kelompok (13452) dengan jarak terdekat 5.
7. Buat Tabel Per Kelompok Hasil Penggabungan
Algoritma complete linkage merupakan algoritma yang menganggap satu data sebagai kluster, Contoh diatas itu menggunakan data yang berjumlah 5, artinya di tahap awal ada 5 kluster
5 kluster = 1,2,3,4,5
Pada tahap pertama, data ke 1 dan data ke 3 bergabung menjadi data (1,3) sehingga data berjumlah 4 kluster
4 kluster = (1,3),2,4,5
Pada tahap kedua, data ke 4 dan data ke 5 bergabung menjadi data (4,5) sehingga data berjumlah 3 kluster
3 Kluster =(1,3),2,(4,5)
Pada tahap ketiga, data (4,5) dan data ke 2 bergabung menjadi data (4,5,2) sehingga data berjumlah 2 kluster
2 Kluster = (1,3),(2,4,5)
Pada tahap keempat, data (2,4,5) dan data (1,3) bergabung menjadi data (1,2,3,4,5) sehingga data berjumlah 1 kluster
1 Kluster = (1,2,3,4,5)
Algoritma berakhir ketika semua data bergabung dalam satu kluster, atau menjadi 1 kluster
Menghitung RMMTD Dan Rs
1. Untuk 5 Cluster
| Kluster | No | Data X | Data Y | Rata-Rata X | Rata-Rata Y | Mean Corrected X | Mean Corrected Y | Jumlah |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 |
|
|
|
|
|
|
|
|
|
|
| Kluster | No | Data X | Data Y | Rata-Rata X | Rata-Rata Y | Mean Corrected X | Mean Corrected Y | Jumlah |
| 2 | 2 | 4 | 1 | 4 | 1 | 0 | 0 | 0 |
|
|
|
|
|
|
|
|
|
|
| Kluster | No | Data X | Data Y | Rata-Rata X | Rata-Rata Y | Mean Corrected X | Mean Corrected Y | Jumlah |
| 3 | 3 | 1 | 2 | 1 | 2 | 0 | 0 | 0 |
|
|
|
|
|
|
|
|
|
|
| Kluster | No | Data X | Data Y | Rata-Rata X | Rata-Rata Y | Mean Corrected X | Mean Corrected Y | Jumlah |
| 4 | 4 | 3 | 4 | 3 | 4 | 0 | 0 | 0 |
|
|
|
|
|
|
|
|
|
|
| Kluster | No | Data X | Data Y | Rata-Rata X | Rata-Rata Y | Mean Corrected X | Mean Corrected Y | Jumlah |
| 5 | 5 | 5 | 4 | 5 | 4 | 0 | 0 | 0 |
2. Untuk 4 Cluster
| Kluster | No | Data X | Data Y |
| 1 | 1 | 1 | 1 |
| 3 | 1 | 2 | |
| Rata-rata | 1 | 1,5 | |
| Mean Corrected 1 | 0
rumusnya =(1-0)^2 |
0,25
rumusnya =(1-1,5)^2 |
|
| Mean Corrected 2 | 0
rumusnya =(1-0)^2 |
0,25
rumusnya =(2-1,5)^2 |
|
| Jumlah Mean Corrected | 0
rumusnya = total mean corrected |
0,5
rumusnya = total mean corrected |
|
| Jumlah | 2 | ||
| Kluster | No | Data X | Data Y |
| 2 | 2 | 4 | 1 |
| Rata-Rata | 4 | 1 | |
| Mean Corrected | 0 | ||
| Jumlah Mean Corrected | |||
| Jumlah | |||
| Kluster | No | Data X | Data Y |
| 3 | 4 | 3 | 4 |
| Rata-Rata | 3 | 4 | |
| Mean Corrected | 0 | ||
| Jumlah Mean Corrected | |||
| Jumlah | |||
| Kluster | No | Data X | Data Y |
| 4 | 5 | 5 | 4 |
| Rata-Rata | 5 | 4 | |
| Mean Corrected | 0 | ||
| Jumlah Mean Corrected | |||
| Jumlah | |||
3. Untuk 3 Cluster
| Kluster | No | Data X | Data Y |
| 1 | 1 | 1 | 1 |
|
|
3 | 1 | 2 |
| Rata-rata | 1 | 1,5 | |
| Mean Corrected 1 | 0 | 0,25 | |
| Mean Corrected 2 | 0 | 0,25 | |
| Jumlah Mean Corrected | 0 | 0,5 | |
| Jumlah | 2 | ||
| Kluster | No | Data X | Data Y |
| 2 | 2 | 4 | 1 |
| Rata-Rata | 4 | 1 | |
| Mean Corrected | 0 | ||
| Jumlah Mean Corrected | |||
| Jumlah | |||
| Kluster | No | Data X | Data Y |
| 3 | 4 | 3 | 4 |
|
|
5 | 5 | 4 |
| Rata-rata | 4 | 4 | |
| Mean Corrected 1 | 1 | 0 | |
| Mean Corrected 2 | 1 | 0 | |
| Jumlah Mean Corrected | 2 | 0 | |
| Jumlah | 2 |
|
|
4. Untuk 2 Cluster
| Kluster | No | Data X | Data Y |
| 1 | 1 | 1 | 1 |
|
|
3 | 1 | 2 |
| Rata-rata | 1 | 1,5 | |
| Mean Corrected 1 | 0 | 0,25 | |
| Mean Corrected 2 | 0 | 0,25 | |
| Jumlah Mean Corrected | 0 | 0,5 | |
| Jumlah | 2 | ||
| Kluster | No | Data X | Data Y |
| 3 | 4 | 3 | 4 |
| 5 | 5 | 4 | |
| 2 | 4 | 1 | |
| Rata-rata | 4 | 3 | |
| Mean Corrected 1 | 1 | 1 | |
| Mean Corrected 2 | 1 | 1 | |
| Mean Corrected 3 | 0 | 4 | |
| Jumlah Mean Corrected | 2 | 6 | |
| Jumlah | 4 | ||
5. Untuk 1 Cluster
| Kluster | No | Data X | Data Y |
| 1 | 1 | 1 | 1 |
| 3 | 1 | 2 | |
| 4 | 3 | 4 | |
| 5 | 5 | 4 | |
| 2 | 4 | 1 | |
| Rata-rata | 2,8 | 2,4 | |
| Mean Corrected 1 | 3,24 | 1,96 | |
| Mean Corrected 2 | 3,24 | 0,16 | |
| Mean Corrected 3 | 0,04 | 2,56 | |
| Mean Corrected 4 | 4,84 | 2,56 | |
| Mean Corrected 5 | 1,44 | 1,96 | |
| Jumlah Mean Corrected | 12,8 | 9,2 | |
| Jumlah | 8 | ||
Menghitung J.Cluster Terbaik
| UNTUK 5 KLUSTER | |
| JUMLAH MEAN CORRECTED | 0 |
| JUMLAH | 0 |
| RMSSTD | 0 |
| TOTAL MEAN CORRECTED | 22 |
| R-SQUARED | 1 |
| UNTUK 4 KLUSTER | |
| JUMLAH MEAN CORRECTED | 0,5 |
| JUMLAH | 2 |
| RMSSTD | 0,5 |
| TOTAL MEAN CORRECTED | 22 |
| R-SQUARED | 0,977272727 |
| UNTUK 3 KLUSTER |
| JUMLAH MEAN CORRECTED |
| JUMLAH |
| RMSSTD |
| TOTAL MEAN CORRECTED |
| R-SQUARED |
| UNTUK 2 KLUSTER | |
| JUMLAH MEAN CORRECTED | 8,5 |
| JUMLAH | 6 |
| RMSSTD | 1,190238071 |
| TOTAL MEAN CORRECTED | 22 |
| R-SQUARED | 0,613636364 |
| UNTUK 1 KLUSTER |
|
| JUMLAH MEAN CORRECTED | 22 |
| JUMLAH | 8 |
| RMSSTD | 1,658312 |
| TOTAL MEAN CORRECTED | 22 |
| R-SQUARED | 0 |
Hasil Akhir RMMSTD DAN R-SQUARED
| JUMLAH KLUSTER | RMSSTD | R-SQUARED |
| 1 | 1,658312395 | 0 |
| 2 | 1,190238071 | 0,61363636 |
| 3 | 0,790569415 | 0,88636364 |
| 4 | 0,5 | 0,97727273 |
| 5 | 0 | 1 |
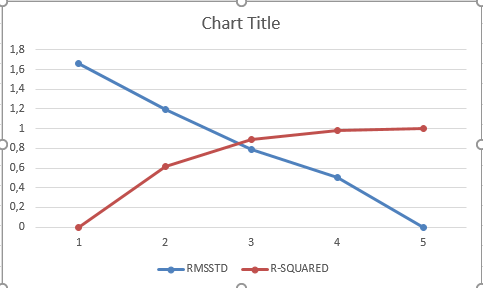
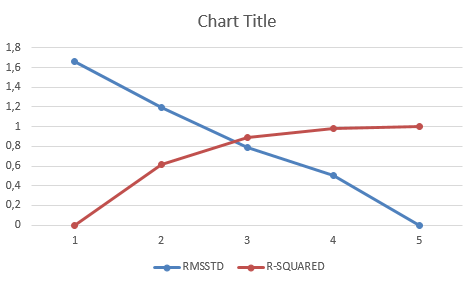
TERJADI PERPOTONGAN DI JUMLAH KLUSTER 3, MAKA JUMLAH KLUSTER TERBAIK ADALAH 3
Download Simulasi Perhitungan Disini
Judul Skripsi Lainnya
Sistemit24.com

Bingung Dengan Algoritma?
Jangan kawatir Sistemit24.com dapat membantu kalian dalam membuat tugas akhir, Dijamin sampai benar-benar selesai.
- Tidak ada batasan untuk revisi
- Dibimbing sampai benar-benar faham
Kami dapat membuatkan dari awal sampai selesai.
Berminat? bisa hubungi kami lewat email : [email protected] Atau hubungi lewat wa 0823-8560-3528
 Shared
Shared
 Shared
Shared
 Shared
Shared
 Shared
Shared